数论研究者中好像有一种有意避开谈“除以0”和“无穷大/小”的倾向,因为以往的数论研究者们没有把数论做为包含在群论和抽象代数中的一门学问来对待。数论中研究的数,只能反应多维的数字空间在一维中、一条坐标轴中的投影。当一个数除以0的时候,正像多年前有人提出-1的平方根等于i以后,一维中的数与另一维中的数就被联系起来了。只有这样,数论的研究发展才能达到更完善。
而下面的公式也正好展示了到今天为止,数论研究中所缺乏和需要的。
x / 0 = y (坐标系之间的“感应”:电磁;风雨)
0 / 0 = h (因为0=h*0,测不准原理,历史中总有一定成份的虚假)
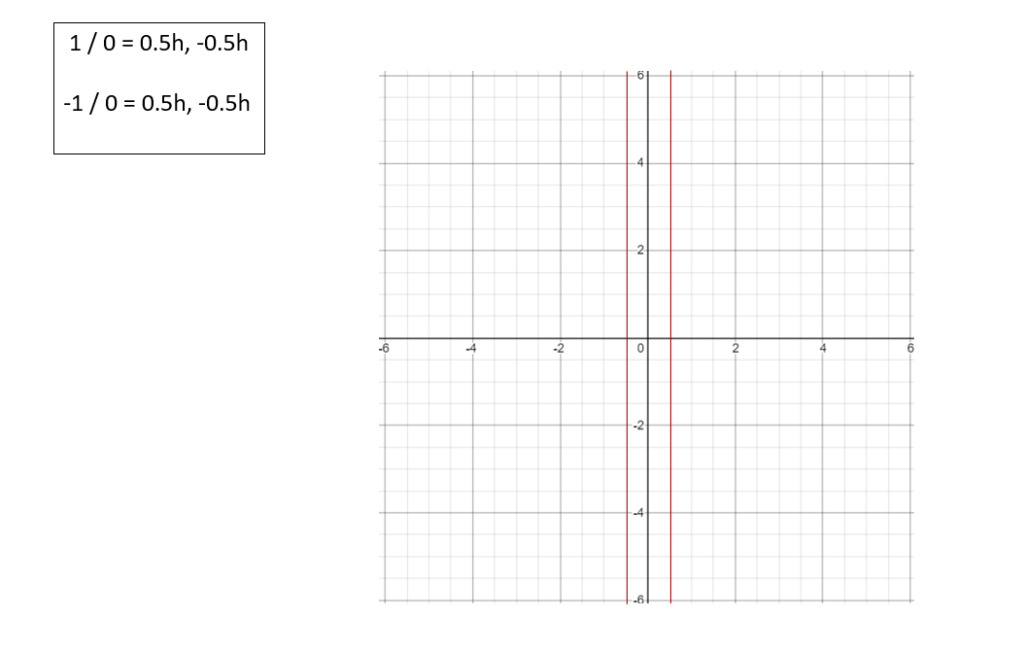
1 / 0 = 0.5h, -0.5h (确立“悟空数”的单位“h”,以及自然数的最小量子化间隔为0.5h)
-1 / 0 = -0.5h, 0.5h (与上同)
A ≡ A (同一维中,自己恒等于自己)
A ≢ B (不同一维中,有条件的相等不是恒等)
应该说:有了以上公式以后,数论做为一个数学理论才变得更加成熟和更能反应宇宙的现实。不惧怕谈“无限大”、“无限小”之后,一些数论的猜想,如:黎曼猜想,哥德巴赫猜想,孪生质数猜想……也就可以得到轻易的证实。
下面看一看 x / 0 = y 是怎么推导出来的?
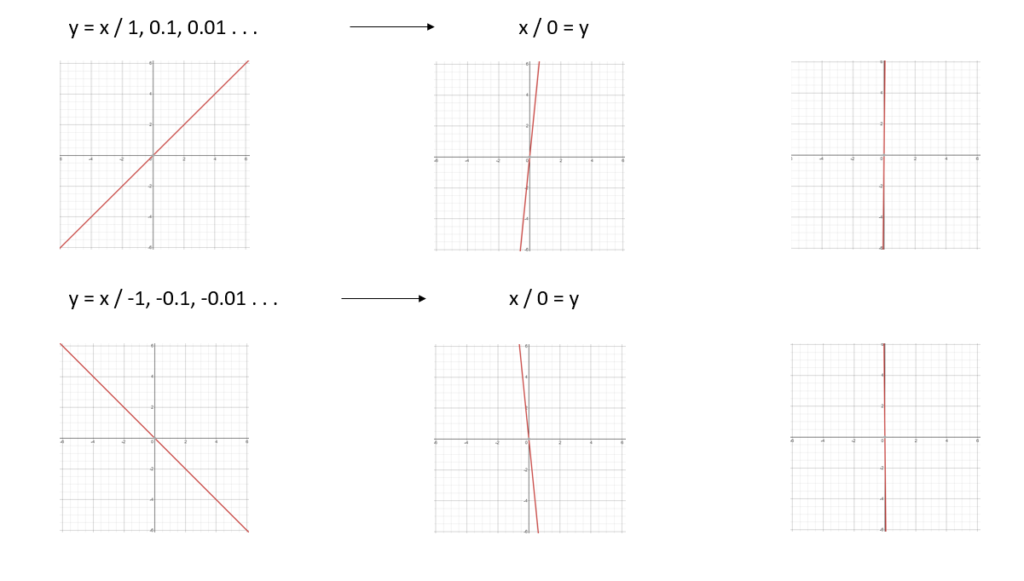
现在让我们来看看思维、进化 的“悟空”数的单位 h (history),是怎样建立的?。因为这新的一维 “y” 是从两个不同的方向,演化合并而来的。那么这个新的单位 “1h” 也就被数字 “0” 给从中对半分开了。
以上推到演化和建立“悟空数”的单位 “h” 的过程,就是黎曼猜想成立的证据。黎曼猜想是一个跨越两“维”之间(实数&虚数“维”)观察到的现象。我们现在也跨越两“维”之间(实数&悟空数“维”)观察到了同样的现象。根据相对论的原则,坐标系统之间,也就是维与维之间,在抽象代数中是地位均等可以互相替代的。
如同在复数系统中,有“实部”和“虚部”一样,在悟空数系统中,也有“实部”和“空部”。 于是证明哥德巴赫猜想的数学问题也就变成了:如何证明在悟空数所组成的“群”中,”1+ah = 0.5+bh + 0.5+ch” 在“实部”是相等的。1=0.5+0.5,这还用证明吗?简直是不言自明啊!
对了,不能忘了证明“孪生质数猜想”。几千年前欧几里得已经证明过在自然数中有无穷多个质数。上面我们提到了,在二维的时空中的观察现象是,大于3的质数间的最小间隔“1h”,投影在自然数范围内是“2”,这是一个“模”的尺寸、内维数。所以在自然数的集合中也就会有无穷多对孪生质数。不然我们就浪费了欧几里得聪明的反证法和令人信服的证明,或者试图用自然数的后半部改变前半部中定义的“1h”或“2”的最小间隔模量维数。得到的矛盾的结果是不可能成立的。